이번 포스트에서는 크루스칼 알고리즘을 다루도록 하겠습니다
긴호흡의 글이 될 것 같아 3개의 글로 나눠 포스트 하도록 하겠습니다.
이번 포스트에서는 크루스칼알고리즘의 개념을 이해하는데 중점을 두고 구현은 다음 글에서 작성하도록 하겠습니다.
(게시글의 자료들은 잔재미코딩(https://www.fun-coding.org/Chapter20-prim-live.html) 사이트를 참조하였습니다)
먼저 크루스칼 알고리즘을 이해하기 위해서 최소 신장트리의 개념을 알아야 합니다.
왜냐면 크루스칼 알고리즘이 어떠한 그래프가 주어졌을 때 그래프의 최소신장 트리를 찾아내는 알고리즘이니까요
신장 트리(Spanning Tree) 란?
-
원래의 그래프의 모든 노드가 연결되어 있으면서 트리의 속성을 만족하는 그래프
-
신장 트리의 조건
- 본래의 그래프의 모든 노드를 포함해야 함
- 모든 노드가 서로 연결
- 트리의 속성을 만족시킴 (사이클이 존재하지 않음
이 부분은 그림을 보시면 한눈에 확인 할 수 있습니다.

보시는 바와같이 그래프의 모든노드가 빠짐없이 이어져 있으며, 각 간선들이 사이클을 생성하지 않습니다, 사이클이란 쉽게 말하면 간선들이 이어진 모양이 태두리로 둘러싸여 막힌 모양이라고 생각하시면 되겠습니다.
그렇다면 최소신장트리란 무엇인지 감이 오시나요?
최소 신장 트리
- Minimum Spanning Tree, MST 라고 불리움
- 가능한 Spanning Tree 중에서, 간선의 가중치 합이 최소인 Spanning Tree를 지칭함
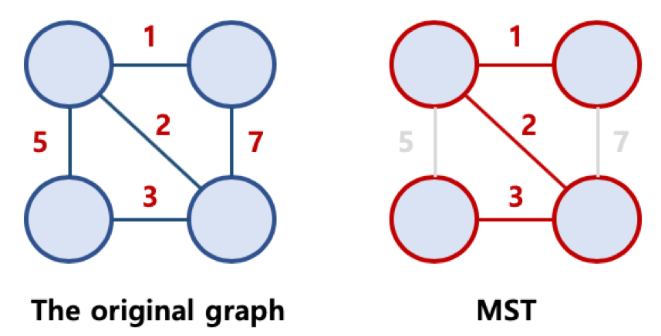
왼쪽과 같이 간선에 가중치가 설정된 original그래프가 있다고 가정합시다. MST란 이 가중치가 설정된 그래프에서
spanning tree를 구현하였을 때 각 간선들의 가중치합이 가장작은 신장트리를 의미합니다. 만약 최소 가중치합 6이라 가정했을때 신장트리중에 가중치 합이 6인 트리가 여러개라면, MST도 여러개 존재할 수 있습니다. 위 예시에서는 하나만 존재하는군요
따라서 이번 포스트에서 알아볼 크루스칼 알고리즘이란 어떠한 그래프가 주어졌을 때 최소 신장 트리를 찾을 수 있는 알고리즘입니다. 대표적인 최소 신장 트리 알고리즘은 Kruskal’s algorithm (크루스칼 알고리즘), Prim's algorithm (프림 알고리즘)이 있는데, 순차적으로 알아보도록 하겠습니다.
크루스칼 알고리즘 (Kruskal's algorithm)
- 모든 정점을 독립적인 집합으로 만든다.
- 모든 간선을 비용을 기준으로 정렬하고, 비용이 작은 간선부터 양 끝의 두 정점을 비교한다.
- 두 정점의 최상위 정점을 확인하고, 서로 다를 경우 두 정점을 연결한다. (최소 신장 트리는 사이클이 없으므로, 사이클이 생기지 않도록 하는 것임)
위 단계는 크루스칼 알고리즘을 구현하기 위한 단계를 크게 분류해 놓은겁니다.
당장은 글이 잘 이해가 안될 수 도 있습니다. 먼저 그림으로 어떻게 동작하는지에 대한 개념을 살펴봅시다 .

먼저 모든 간선들이 가중치가 작은순서대로 정렬되어있다고 가정합시다.
따라서 간선의 가중치가 가장작은 A-D 간선을 선택하여 해당 노드를 이어줍니다. 그리고 차례대로 그다음으로 가중치가 같거나 작은 간선을 선택하여 노드를 이어줍니다. 위 예시에서는 E와 C노드가 되겠네요

그 다음으로 가중치가 작은 간선인 D-F노드를 선택합니다. A의 루트노드는 D, B는 독립적인 노드로 자기자신이 루트노드이니, 서로의 루트노드가 다르기 때문에 아래와 같이 트리형식으로 한 집합으로 묶어줍니다. 이 노드들을 묶는 방법에 대해서는 다음 포스트에서 설명할 예정이니 우선 개념적인 부분만 이해하는걸 목표로 합시다 ㅎ

그 다음으로 작은 가중치는 7이므로 먼저 A-B 간선을 추가하여 이어봅시다. A-B 역시 서로 한 집합에 있지않은 독립적인 집합이었으므로 이어주는 것이 가능합니다. A의 루트노드는 D, B는 기존에 없던 독립적인 노드이니 하나로 합쳐주는 것이 가능합니다.
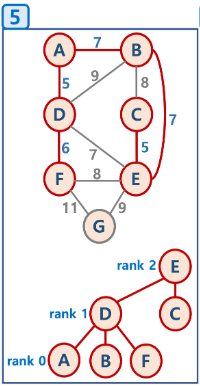
이제 B-E간선을 선택해서 이어봅시다. 마찬가지로 트리에서 각각 B , E 노드의 루트노드가 다르기에 두 집합을 하나로 묶을 수 있습니다.

이제 다음으로 가중치가 작은 D,E 간선을 선택했다고 가정합시다. D,E 를 연결하게 되면 사이클이 생기게 됌을 확인할 수 있습니다. 트리 구조를 확인해 보면 역시나 D의 루트노드는 E, E 노드는 본인이 루트노드 이므로 서로의 루트노드가 같습니다. 즉, D,E는 서로 같은 집합(트리)에 속해있다고 볼 수 있는거지요
이제 왜 간선을 추가 할 떄마다 각 노드를 잇는 집합을 트리로 표시하는지, 감이 조금 오시나요?
크루스칼 알고리즘은 간선을 선택했을 때 간선이 사이클을 생성하는지의 여부를 두 노드가 서로 같은 집합에 속하는지 여부로 판단을 합니다. 이 같은 집합에 속한다는것을 판단하기 위한 도구로 각 간선을 선택할 때 해당노드들을 트리로 만들어 확인하는 겁니다. (이 트리를 생성하는 방법에 대해서는 다음 포스트에서 설명하도록 하겠습니다)

따라서 위와 같은 사이클이 생기는 경우들을 배제하고, 순차대로 가중치가 작은 간선들을 선택해서 묶어주다보면 위와 같이 주어진 그래프에서 MST를 찾아 낼 수 있는겁니다 !
여기까지가 크루스칼 알고리즘이 동작하는 아주 큰 관점에서의 개념을 살펴보았습니다.
다음 포스트에서는 그렇다면 어떤 방식으로 노드들을 묶고 트리를 생성 하는지에 대한 방법을 다루도록 하겠습니다
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [알고리즘, C++]백 트래킹 (Backtracking) (0) | 2020.05.09 |
|---|---|
| [알고리즘, 파이썬] 프림 알고리즘 - 2 (0) | 2020.04.27 |
| [알고리즘 , 파이썬] 프림 알고리즘 - 1 (0) | 2020.04.27 |
| [알고리즘, 파이썬] 크루스칼 알고리즘 - 3 (0) | 2020.04.23 |
| [알고리즘, 파이썬] 크루스칼 알고리즘 - 2 (0) | 2020.04.23 |