[알고리즘, C++]백 트래킹 (Backtracking)

이번 포스팅에서는 백 트래킹 기법에 대해서 포스팅 하도록 하겠습니다. 

사실 백 트래킹이라는 것은 알고리즘이라기 보단 어떤 문제를 풀기위한 전략? 에 가까운데요,

어떤 제약조건 만족 문제에서 해를 찾기 위한 전략으로 백 트래킹(backtracking) or 퇴각 검색(backtrack)으로 부릅니다.

 

해를 찾기 위해, 후보군에 제약 조건을 점진적으로 체크하다가, 해당 후보군이 제약 조건을 만족할 수 없다고 판단되는 즉시 backtrack (다시는 이 후보군을 체크하지 않을 것을 표기)하고, 바로 다른 후보군으로 넘어가며, 결국 최적의 해를 찾는 방법입니다. 

 

실제 구현시, 고려할 수 있는 모든 경우의 수 (후보군)를 상태공간트리(State Space Tree)를 통해 표현

(반드시 트리형태로 만들 필요는 없습니다, 컨셉상 트리를 의미, 뒤에 예제와 함께 설명드리겠습니다. )

• 각 후보군을 DFS(깊이 우선 탐색) 방식으로 확인
• 상태 공간 트리를 탐색하면서, 제약이 맞지 않으면 해의 후보가 될만한 다른 곳으로 바로 넘어가서 탐색
  • Promising: 해당 루트가 조건에 맞는지를 검사하는 기법
  • Pruning (가지치기): 조건에 맞지 않으면 포기하고 다른 루트로 바로 돌아서서, 탐색의 시간을 절약하는 기법

즉, 다시한번 요약하자면 백트래킹은 트리 구조를 기반으로 DFS로 깊이 탐색을 진행하면서 각 루트에 대해 조건에 부합하는지 체크(Promising - 솔루션이 될수 있는지), 만약 해당 트리(나무)에서 조건에 맞지않는 노드는 더 이상 DFS로 깊이 탐색을 진행하지 않고, 가지를 쳐버림 (Pruning - 이 노드 아래의 모든 값들은 탐색할 필요가 없다) 라는 겁니다. 

 

글로봤을 때는 무슨 말인지 잘 와닿지 않겠지만,  예제를 풀다보면 이것들이 무슨 의미인지 좀더 이해가 쉬울겁니다. 이제 백 트래킹 예제를 풀어보면서 살펴보겠습니다.

 

 

N Queen 문제

문제는 다음과 같습니다.

• NxN 크기의 체스판에 N개의 퀸을 서로 공격할 수 없도록 배치하는 문제
• 퀸은 다음과 같이 이동할 수 있으므로, 배치된 퀸 간에 공격할 수 없는 위치로 배치해야 함

 

이 N Queen 문제는 대표적인 백 트레킹 문제입니다. 

만약 4X4 크기의 체스판이라고 가정한다하면 16개의 칸중에 4개의 퀸자리를 선택하는 경우의 수만 해도 

C(16,4) = 1820 , 각 행마다 하나씩 자리를 선택한다하도 4x4x4x4 = 256 가지의 경우의 수가 존재합니다.

 

이 모든 경우의 수를 다 참조하여 솔루션을 판단하는 것은 매우 비효율적이죠, 어디서 부터 시작해야 할지도 참 난감합니다; 우선 위에서 기술한 대로 고려할 수 있는 모든 경우의 수를  State Spae Tree로 표현해 봅시다.

 

 

4 queens problem - State Space Tree

 

State Space Tree로 모든 경우의 수를 표현해본 그림입니다.

(위 그림은 개념적으로 트리형태로 표현한 것이지 구현시 반드시 트리구조를 이용해야하는 것은 아닙니다) 

각 노드의 레벨은 체스판의 행번호와 같습니다.  [1,1] 노드는 레벨이 1이므로 1행에 1열에 Queen을 배치하겠다는 의미입니다.  그림에서 보이는 것과 같이 [3,4]은 [1,1], [2,1] 상태에서 추가적으로 [3,4] 위치에 퀸을 배치된 상태를 의미합니다.  

 

이제 Promising한 노드와 non-promising 한 경우를 살펴 봅시다.

 

non-promising 노드들을 puned(가지치기)한 state space tree

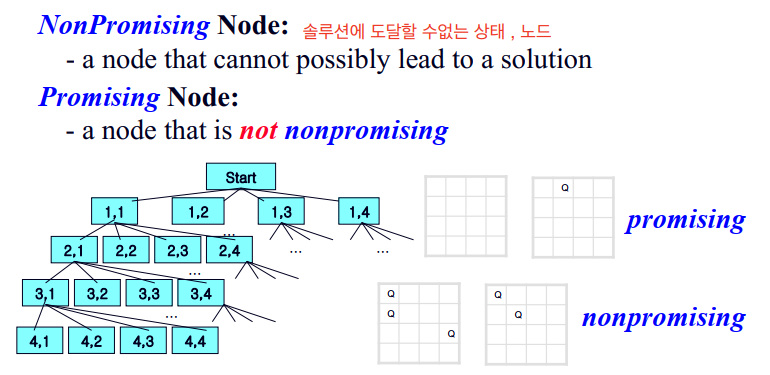
그림이 조금 난해합니다; 

이 문제에서 promising 한것은 해당 노드가 배치된 퀸들끼리 서로의 공격범위에 들어가있지 않은 상태를 의미합니다.

예를 들면 위 그림과 같이 [1,2] 노드 상태는 아직 퀸하나만 배치되어 있으므로 promising 조건을 만족합니다. 

(즉 그대로의 의미처럼 이 밑으로 솔루션이 나올수 있는 유망한 노드라는 뜻입니다.)

이럴경우 해당 노드의 밑으로 계속해서 깊이 우선탐색을 진행합니다. 

 

하지만 non-promising, 예를 들면 [1,1] -> [2,1] 노드처럼 이미 서로의 공격범위에 노출되어있는 상태의 노드들은 

이 밑으로 경우의수를 탐색해봤자 더 이상 의미가 없습니다. 어차피 이 밑으로 탐색을 진행해도 솔루션을 만족하지 못하는  non-promising (유망하지 않은) 노드라는 것입니다. 이럴경우 [2,1] 밑으로는 탐색을 하지않고 (Pruning, 가지치기다시 backtrack 하여 다른 promising한 노드들을 찾아 조사를 시작합니다. 

 

이제 Backtracking이란 기법이 어떻게 적용되는지 감이 오시나요?  다시한번 요약하자면 아래와 같습니다. 

 

Backtracking

• 기본적으로 깊이 우선 탐색을 실행하지만, 더깊은 노드를 탐색하는 것은 현재 노드가 promising 한지에 달려있다. 
• 만약 non-promising 하다면, backtrack하여 해당 노드의 부모노드로 돌아가 다른 노드를 search 한다  

 

이제 본격적으로 코드를 짜기위해 Promising 한지를 판단하기 위한 규칙을 정의해 보겠습니다.

 

Col(i)를 i행에 위치한 퀸이 위치한 열의 번호라 정의

• 두 퀸이 같은 열에 위치하는 지 check 하려면 :  Col(i) = Col(k) 인지 판단 
• 두 퀸이 서로 같은 대각선에 위치하는지 check 하려면:   |Col(i) - Col(k)| = i-k 인지 판단 

위 조건들을 check해서 두 조건에 해당하지 않는다면 해당 노드는 pomising하다고 판단할 수 있습니다.

이를 기반으로 코드를 작성하면 다음과 같습니다 .

 

1. promising한지를 판단하는 함수구현 

2. promising 한지 체크하며 재귀적으로 깊이 우선탐색을 실행하는 함수  

 

#include <iostream> using namespace std; int N; //체스판 사이즈 int col[15]; int result = 0; bool promising(int i) { for(int j=0;j<i; j++) { if(col[j] == col[i] || abs(col[i]-col[j])==(i-j)) return false; } return true; } void N_qeen(int i) { if(i==N) result +=1; else { for(int j=0 ; j<N, j++) { col[i] = j; if(promising(i)) N_qeen(i+1); } } } int main() { cin>>N; N_qeen(0); cout<<result<<endl; return 0; }

 

코드를 구현하였으니 분석을 진행해볼 시간입니다! 

N-queen 문제의 경우, 정확한 n에 대한 값을 계산하기는 어렵지만 대략적으로

이 정도 이상은 방문하지 않겠다라는 upper bound 값은 계산할 수는 있습니다.

 

먼저 알고리즘을 고려하지 않고 최대 탐색할 수 있는 노드의 수를 계산해보면 

깊이 1에는 -> 1개 

깊이 2에는 -> n개 ,

깊이 3에는 각 노드에서 또 n개 씩 가지가 나온다고 가정하면 -> $ n^2 $ 

이런 식으로 깊이 n까지 나아간다면 최대로 탐색할 수 있는 노드의 수는 

1 + n + $n^2$ + $n^3$ + ... + $n^n$=($n^{n+1}$-1)/(n-1)

이와 같이 Maximum upper Bound를 정할 수 있습니다.

 

열이 다른 것들을 제외했을 때의 promising 한 노드를 거치는 경우만  따져도 나름 대로

upperbound을 계산할 수 있으니 따져보면 

 

Upper Bound on number of pormising nodes :

깊이 1 -> 1

깊이 2 -> n

깊이 3 -> $n\times (n-1)$  (열이 겹치는 경우를 하나 뺀경우)

깊이 4 ->  $n\times (n-1)\times (n-2)$

이 모든 경우를 더하면 1+ n + n(n-1) + .. + n! 임을 알 수 있습니다.  

 

 

Graph Coloring 문제

문제는 다음과 같습니다.

• 어떤 방향성이 없는 그래프가 주어졌을 때, 그래프의 각 노드에 m개의 색깔중 하나를 선택해서 칠함 
• 서로 인접한 노드의 색깔은 같은 색이 되지 않도록 칠해야 한다. 

처음 접했을 때는 어떻게 접근해야 할지 막막하지만 왼쪽그림을 오른쪽과 같이 그래프로 표현할 수 있다는 점을

깨닫는 다면 쉽게 접근이 가능합니다. 이제 오른쪽 그림과 같은 그래프를 토대로 상태공간트리를 표현해보겠습니다. 

 

각 단계를 (level을) 노드라고 정의한다면 오른쪽과 같이 상태공간 트리를 표현할 수 있습니다. 

이제 state space tree를 정의하였으니 이것을 토대로 탐색을 계속 진행할지 여부를 반단하는 promising함수와 

promising한 노드를 재귀적으로 탐색할 backtracking 함수를 구현하기만 하면 됩니다. 

 

먼저 backtracking 부분을 구현해 봅시다. 

backtracking 함수를 구현할 때 필요한 부분은 다음 두가지 입니다. 

 

1. 모든 탐색이 끝났을 때 탐색을 종료하는 분기점 

2. promising하다면 해당노드로 다음탐색을 진행하는 부분 

 

위 두가지 내용을 반영하여 backtracking 함수를 구현하면 다음과 같습니다. 

 

#include <iostream> using namespace std; int N = 4 ; int W[4][4]; int result[4]; int COLOR = 3; void backtracking(int node) { if(promising(node)){ if(node == N){ //cout<<result[1] ~ result[4] 결과값 출력 } else{ for(int color=0; color<COLOR ; color++){ result[node+1] = color; backtracking(node+1); } } } }

 

 

이제 promising 함수를 구현해봅시다.

promising한 조건을 만족하지 못하는 경우는 어떤경우가 있을까요?

아마 어느 두 노드가 서로 이어져있고, 이어져 있는 두 노드가 같은 색깔을 갖는다면 그것은 promising 하지 않은 상태일 겁니다. 이를 간단한 코드로 구현한다면 다음과 같이 표현할 수 있습니다.

 

#include <iostream> bool promising(int i){ int j=1; int Switch =true; while(j<i && Switch){ if(W[i][j] && result[i]==result[j]) Switch = false; j++; } return Switch }

 

 

The 0-1 Knapsack 문제

문제는 다음과 같습니다.

• 배낭에 담을 수 있는 무게의 최댓값은 정해져 있다. 
• 배낭에 넣을 물건들은 각자 무게와 가치가 정해져 있다.
• 짐들을 배낭에 넣을 때 가치의 합이 최대가 되도록 집을 고르는 방법을 찾아라 

앞서 나온 문제들이 백 트레킹으로 특정 결과값을 구하는 문제였다면 이 문제는 앞의 문제들과는 조금 다릅니다. 

바로 특정 값을 구하는 것이 아닌 조건을 만족하는 해중 가장 최적의 해를 찾는 문제라는 겁니다. 

 

우선 state space tree를 어떻게 정의할 지 생각해봅시다. 

최적의 값을 비교하기 위해선 우선 현재의 노드가 가지고 있는 현재 가치(profit)와 무게(weight)에 대한 정보가 필요할 겁니다.  하지만 이것만으로는 state space tree를 생각하기 쉽지 않습니다.  백트레킹을 구현하기 위해서는 필요없는 노드들을 pruning 할 수 있는 조건이 필요한데, 위 두 정보만으로는 이를 구현하기 어렵기 때문이죠..

따라서 다음과 같은 정보를 상태공간 트리 노드에 추가해 줍니다. 

 

The upper bound on the maximum profit

-> 물픔을 조각내어(fraction) 채워넣는것을 허용하였을 때, 현재 노드에서 향후 얻을 수 있는 최대 이득값  

 

말이 조금 애매할 수 있지만, 정리하자면 현재 노드의 가능성, 즉 현재상태에서 최대로 얻을 수 있는 이득값(upper bound)를 계산하여 정보를 가지고 있다면, 탐색중 만약 현재 노드의 upper bound 보다 큰 가치(profit)값을 가지고 있는 다른노드가 존재 한다면,  현재 노드 아래의 값은 더 이상 최적이 값이 아니며 탐색할 필요가 없다는 뜻이 되므로 필요없는 노드들을 pruning 하고  backtracking을 할 수 있게 되는 겁니다.  

 

이제 profit, weight , upper bound 값을 포함한 노드를 토대로 state space tree를 정의해 봅시다. 

 

0-1 knapsack 문제 space state tree

각 물품들은 무게대비 가격이 높은 순으로 정렬되어 있으며, 최대 무게 제한은 16입니다. 

upper bound란 값은 노란색 말풍선 처럼 계산 됩니다. 물품은 위에서부터 아래로 순차적으로 채워지며 

 

item1 -> 이득 : 40 , 무게 : 2  =>  누적무게: 2  

item2 -> 이득 : 30 , 무게 : 5  =>  누적무게: 7  

item3 -> 이득 : 50 , 무게 : 10  =>  누적무게: 17  -> 무게 초과로 fraction 해서 채워넣는다. 

item3 -> 이득: 50 * 9/10, 무게 10* 9/10 => 누적 무게 16 , 총 upperbound profit = 115

(9/10은 (16 - 7) / item3의 무게로 구한 값)  

 

위와 같은 계산과정을 통해서 계산이 됩니다. 따라서 위 space state tree를 기반으로 

Upper bound 계산하는 부분과 promising 함수를 정의 할 수만 있다면,

이 문제를 backtracking으로 해결 할 수 있을 겁니다. 

 

백트래킹 함수 부분: 

최적의 값이 나오면 값을 갱신. 

i 레벨까지 (i번쨰 아이템을 넣었을 떄) promising 하다면,

다음 아이템(i+1)을 넣거나, 넣지않았을 경우 2가지에 대해서

재귀적으로 backtracking 함수 호출 

 

#include <iostream> //global variables int maxProfit = 0; //최대 이득값 저장 int numBest = 0; char bestSet[4]; //최적의 값을 갖는 노드의 물품 구성 저장 char curruent_Set[4]; // 예시 | y | y | n | y | int p[4] //문제에서 주어지는 물품의 profit 정보 int w[4] // 문제에서 주어지는 물품의 weight 정보 void backtracking(int i , int profit int weight){ if (weight <= W && profit > maxProfit) { maxProfit = profit; numBest = i; bestSet = current_Set ; } if(promising(i)){ current_Set[i+1] = "y"; backtracking(i+1, profit+ p[i+1], weight+ w[i+1]); current_Set[i+1] = "n"; backtracking(i+1,profit, weight); } }

 

promising 함수 부분: 

만약 현재 무게가 W=16을 초과한다면 false 반환, 

아니라면 upper bound값을 계산해서 현재의 upperbound가 maxProfit값보다 크다면 true 반환 

#include <iostream> bool promising(int i){ if(weight >= W) return false; else{ // upper bound 를 계산하는 부분 j = i+1 ; bound = profit; totWeight =weight; while(j<=n && totWeight+ w[j] <=W ){ totWeight += w[j]; bound += p[j]; j++; } k = j; if (k <= n) bound = bound + (W-totWeight)*p[k]/w[k]; return bound > maxProfit; // upper bound 가 maxprofit 보다 크면 참을 반환 } }

 

이로서 백트레킹에 대한 대표 예제들에 대해서 살펴보았습니다. 

백트레킹으로 문제를 접근하기 위해선 먼저 space state tree를 정의해야 하며

이를 토대로 backtrack함수와 promising 함수를 정의하면 보다 쉽게 문제를 해결할 수 있음을 알아보았습니다.

다음 포스트에서는  Branch and Bound (분기 한정법) 에 대해서 알아보도록 하겠습니다.